Non-interactive Pictures

|
This page shows some fancy 3-D pictures of 2-D wavelets. |
Interactive wavelet demonstrations
Below are some interactive demonstrations of various wavelet properties and in particular
the Dual-Tree complex wavelets.
Notes w.r.t. the use of the applets:
- The latest Java version is required in order to view these applets. In case the latest Java version is not available, you will be redirected to the Java download website.
- Because of security reasons, the Java runtime environment will automatically block applets. So in order to run the applets, you will need to add a security exception on your computer:
- Windows: Control Panel -> Java -> Security -> Exception Site List -> add http://telin.ugent.be.
- MAC OS X: System Preferences -> Java -> Security -> Exception Site List -> add http://telin.ugent.be.
- Linux: use the jcontrol command.
- Note: Recent browsers (Firefox v.53, Chrome v.42, or newer versions) no longer support embedding java applets in HTML pages. Instead, you can download and unzip the software and execute the applets locally through the provided batch scripts: click here. Note that this still requires a local Java Runtime Environment installation.
1. Wavelets |
|
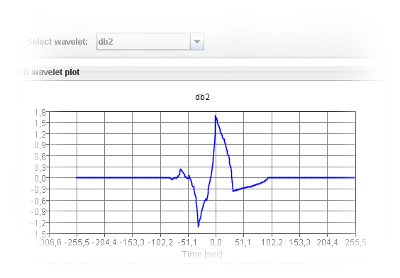
|
Visualization of 1-D wavelets Shows a visual representation of various 1-D wavelets: Daubechies wavelets, Symmlets, Coiflets, ... |
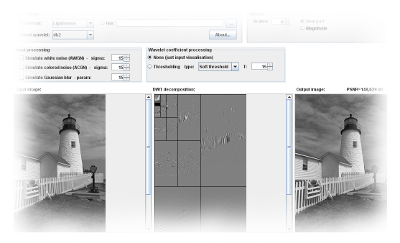
|
2D Discrete Wavelet Transform (DWT)
of images Explore the use of the DWT as an efficient tool for image representation. On this page, you can generate images with simulated Gaussian noise (white or colored) and Gaussian blur. Next, you can investigate the effect of soft/hardthresholding on the wavelet coefficients and you can see the reconstructed image. |
2. Complex Wavelets |
|
| During the last decades, many alternative multiresolution representations have been developed in order to give a solution to the previously mentioned problems with the DWT. One such transform is the dual-tree complex wavelet transform (DT-CWT) [Kingsbury, 2001], which is very related to the DWT and which also provides a multiresolution analysis. | |
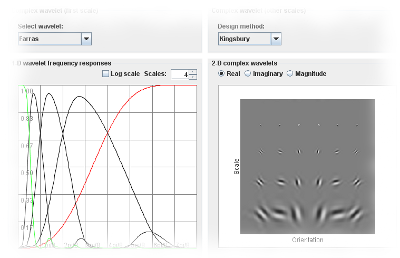
|
Complex Wavelet Browser Allows you to inspect the properties of a number of complex wavelets: spatial localization, frequency localization, directional selectivity. This page also allows you to design your favorite complex wavelet on the fly, using existing design techniques from literature. |
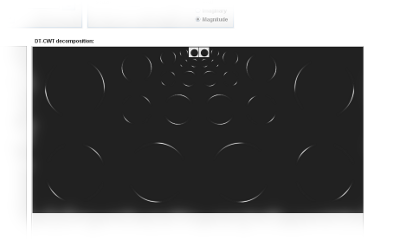
|
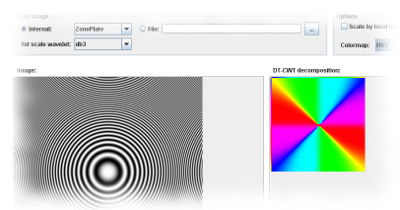
Dual-Tree Complex Wavelet decomposition
of an image Shows the full DT-CWT decomposition of an image into different scales and orientation bands. Applied to standard images like the zoneplate image, this gives a good idea of the directional analysis capabilities of this transform. |
|
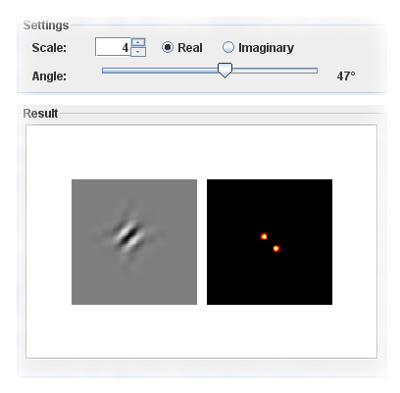
Estimation of the locally
dominant orientation of edges in an image Here we estimate the locally dominant orientation of edges in the image, based on information in different orientation bands on the first scale of the DT-CWT. |
|
Steering Dual-Tree Complex Wavelets:
is this possible?
On this page, we investigate whether it is possible to steer complex wavelet basis functions (and to what extent). A 2-D function is called steerable when it can be written as a linear sum of a fixed number of rotated versions of itself. |
3. Steerable Pyramids |
|
| The steerable pyramid (STP) transform [Simoncelli et al., 1992, Simoncelli and Freeman, 1995] is a 2D multiresolution transform that, like the DT-CWT, has been introduced to overcome limitations of the DWT. | |
|
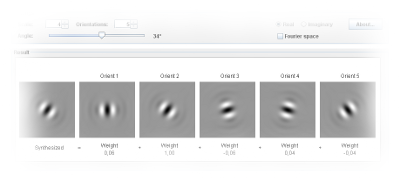
Steering the Steerable Pyramid Transform
filters
Steerable filters in any orientation can be synthesized as a linear sum of a fixed number of rotated versions of itself. This is illustrated in this example. |
4. Shearlets |
|
| The shearlet transform, is a very recent sibling in the family of geometric image representations and provides a traditional multiresolution analysis. By a specific design of the discrete shearlet transform that we use, a lower redundancy factor is possible than with most other multiresolution representations, while offering an excellent directional analysis and even shift invariance. | |
|
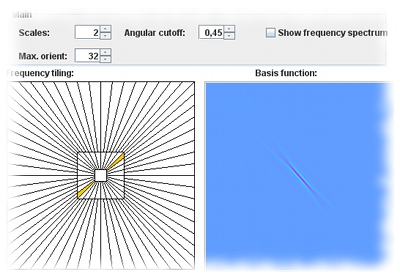
Plot of shearlet basis functions
This applet shows a visualization of different shearlet basis functions (spatial domain + frequency domain). |
Publications
- B. Goossens, J. Aelterman, H. Luong, A. Pizurica and W. Philips, "A split-augmented Lagrangian Algorithm for Spectral Factorization of a set of 2D Directional Filters and Application to the Design of Compact Shearlet Frames," SPIE Optics & Photonics, Wavelets And Applications XV, San Diego, Aug. 25-29, 2013, p. 86730J.1-12.
- B. Goossens, J. Aelterman, H. Luong, A. Pizurica and W. Philips, "Design of a Tight Frame of 2D Shearlets Based on a Fast Non-iterative Analysis and Synthesis Algorithm, " SPIE Optics & Photonics 2011, Wavelets and Sparsity XIV, Aug. 21-25, San Diego, CA, USA, p. 81381Q (13 pages).
- B. Goossens, H. Luong, J. Aelterman, A. Pizurica and W. Philips, "Efficient Multiscale and Multidirectional Representation of 3D Data using the 3D Discrete Shearlet Transform, " SPIE Optics & Photonics 2011, Wavelets and Sparsity XIV, Aug. 21-25, San Diego, CA, USA, p. 81381Z (13 pages).
- B. Goossens, J. Aelterman, H. Q. Luong, A. Pizurica and W. Philips, "Efficient Design of a Low Redundant Discrete Shearlet Transform, " in Proc. 2009 International Workshop on Local and Non-Local Approximation in Image Processing (LNLA2009), August 19-21, 2009, Tuusula, Finland, p. 112-124.
Links
Wavelets
Steerable pyramids
- Steerable filters and the Steerable Pyramid on the website of dr. Filip Rooms.
Shearlets
 website
website