Image restoration

Overview

Colored noise in images
Non-Local Means denoising (NLMeans)
Complex Wavelet-based demosaicing
Links

Non-Local Means source code available (see below)!

Colored noise in images

Despite of the fact that many techniques from literature are designed and quite effective for white (uncorrelated) noise, there is a model mismatch when these methods are applied to "real-life" images, which mostly contain correlated noise.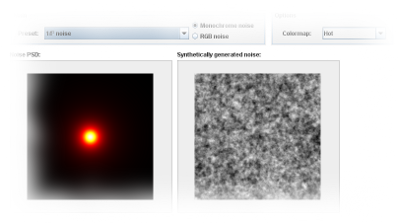


	Demonstration of colored noise Explore different types of colored noise. You can see the Power Spectral Density of the noise together with artificially generated Gaussian noise. Java 6 runtime environment required.

References:

J. Aelterman, B. Goossens, A. Pizurica and W. Philips, "Suppression of Correlated Noise", in Recent Advances in Signal Processing, IN-TECH 2009, ISBN 978-953-307-002-5, p. 211-236, 2009.

Non-Local means denoising (NLMeans)

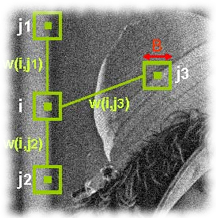
non-local means

The non-local means algorithm is a relatively simple algorithm that averages over groups of blocks that are similar, according to some block distance measure (usually mean square difference, MSD). The algorithm uses therefore information from the whole image to estimate one single pixel. The more similar blocks can be found, the better the estimation will be. Unfortunately, the excessive amount of weight computations makes the NLMeans algorithm very slow. For example, denoising a 512x512 image on a 3.0 GHz CPU with 1 Gb RAM using a direct implementation in C takes about 5 hours and 20 minutes.

In our work, we propose techniques to speed up both the computation time and the visual quality:

The use of a bisquare weight function, that reaches 0 as soon as the block distance is larger than a given threshold. This way, dissimilar blocks are disregarded.
The NLMeans algorithm can be considered to be the first iteration of the Jacobian optimization algorithm. Hence, applying the NLMeans algorithm iteratively further reduces the estimation cost function.
An extension of the algorithm to colored noise. The original NLMeans algorithm only deals with white noise (with a flat power spectrum). Unfortunately, this kind of noise is rarely present in real images (such as coming from CCD digital cameras). We have shown that taking the correlatedness of the noise into account vastly improves the denoising performance.
By exploiting the weight symmetry, the computation time can be reduced with a factor 2. Further, by computing the block distances in a sliding way (i.e. using a moving average filter), the algorithm can be made W² times faster for blocks of size WxW, without loss of accuracy.

Below are denoising results for a number of RGB test images corrupted with artificial colored noise. Click on an image to see the result. Computation time is between 20-35 sec. per image, depending on the size of the images.

Barbara

House

Kodim23

Simpsons

Window

Davy's desk (Digital Camera image with CCD noise)

Source code:

MATLAB code is available here.

Our publications:

B. Goossens, H.Q. Luong, A. Pizurica, W. Philips, "An improved non-local means algorithm for image denoising," in 2008 International Workshop on Local and Non-Local Approximation in Image Processing (LNLA2008), Lausanne, Switzerland, Aug. 25-29 (invited paper)
A. Dauwe, B. Goossens, H.Q. Luong, W. Philips, "A Fast Non-Local Image Denoising Algorithm", in Proc. SPIE Electronic Imaging, San José, USA, January 27-31 2008

Complex Wavelet-based Demosaicing

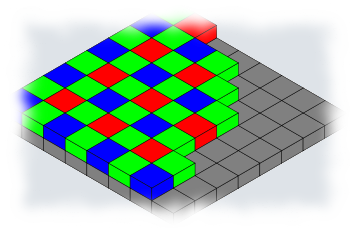
bayer pattern

Most digital cameras capture only one color per pixel (red, green or blue), such as in the so-called Bayer pattern. Demosaicing is the process of interpolating the missing color components of every pixel. One line of research focuses on the frequency-domain view of the demosaicing problem, which leads to linear filter schemes to demultiplex the luminance and chrominance signals. Unfortunately, this sometimes results in errors (orange-blue artifacts in the fence and walls in the figure below), that can also be seen in NTSC/PAL television. Wavelet-based demosaicing (Hirakawa et al.) opens up the possibility to jointly handle the demosaicing and denoising problem in the wavelet domain. This is not only elegant, but allows for a lower computational cost, when compared to state-of-the-art techniques. A disadvantage is that restrictive assumptions are imposed on the power spectral density of the image. When these assumptions are invalid (e.g. for high frequency luminance content), luminance and chrominance crosstalk artifacts appear in the image.

In our work, we take a locally adaptive approach to tackle this problem by making use of the directional and analyticity properties of the Complex Dual-Tree wavelets. Surprisingly, this approach does not increase the computational efficiency significantly and gives a very high visual quality.